Journal of Scientific and Industrial Metrology

Keywords

Optics and photonics; Pulsed lasers; Interferometry; Spectroscopy; FTIR; Optical imaging; Optical coherence tomography

Introduction

Optical sampling is a technique involving the use of a periodic optical signal, often in the form of a high-speed pulse train, to gate the measurement of an electrical or optical signal. It allows a fast temporal signal to be probed by a slow detector, with an operating principle similar to that of a stroboscope. It has been widely used in optical telecommunications and spectroscopy for signal conversion and analysis [1].

Recently, an increasing effort has been devoted to applying optical sampling in precision measurement. This is enabled by the advance in ultrafast lasers and optical frequency combs over the last two decades [2]. A key technical feature of these new schemes is the creation of the Vernier effect in the time domain, often realized by means of two coherent pulse trains with a slight offset in their repetition rates. The detuning generates a rapid scan of the relative pulse delay. Unlike conventional tunable optical delays, such as mechanical-translation delay lines, spinning mirrors and spectral-domain methods, which always suffer from a trade-off between scan rates and scan depths, the optical sampling-based methods are able to achieve high scan rates (up to MHz) and large scan depths (tens of centimeters) simultaneously. This allows precision measurements to be done at unprecedented rates.

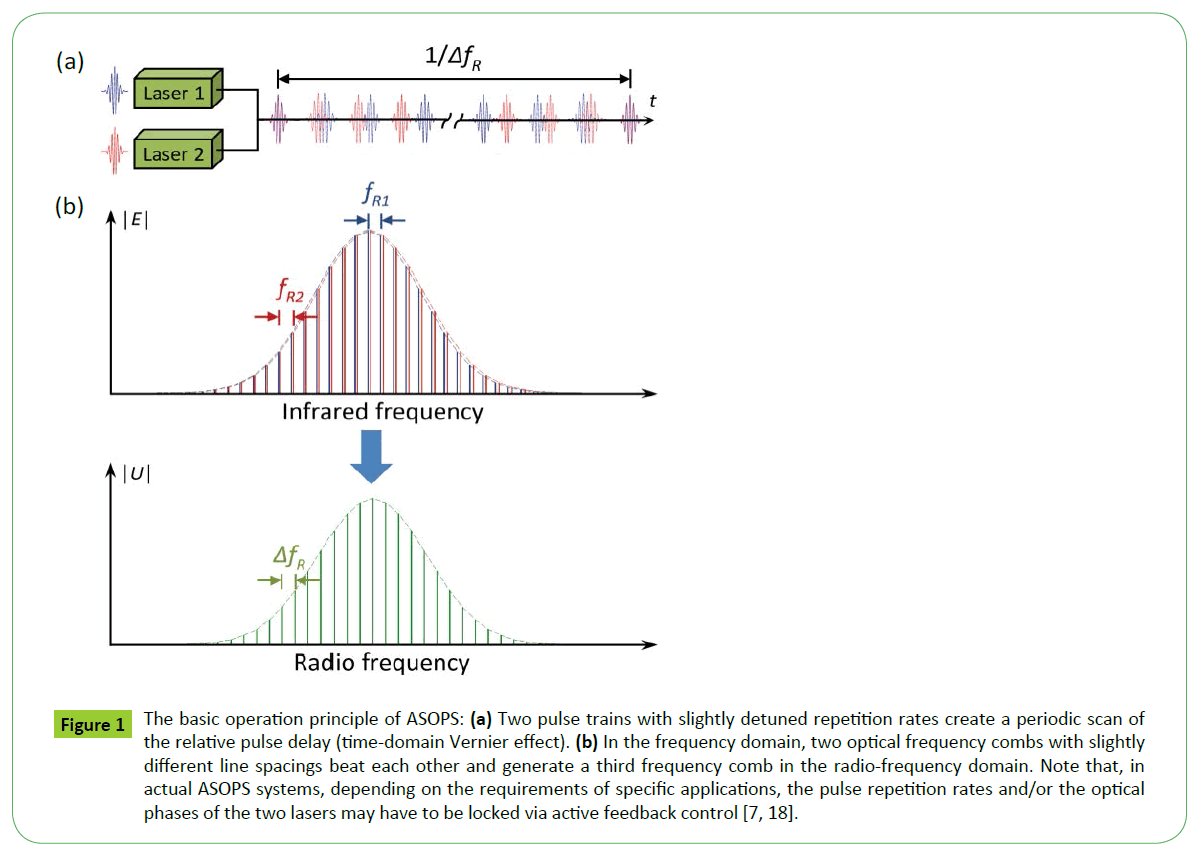
The most widely used scheme among these new techniques is asynchronous optical sampling (ASOPS). Figure 1a illustrates the basic operation principle of ASOPS. Two ultrafast lasers generate two femtosecond pulse trains with slightly detuned repetition rates f_R1 and f_R2 . When the two pulse trains are combined, the relative delay between each pair of pulses gradually “slip” due to the detuning. This pulse-delay slippage repeats at a rate equal to the repetition rate offset 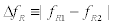, resulting in a periodical scan of optical delay. For example, if two mode-locked lasers operate near 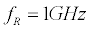, a 0.1% offset between the two repetition rates would lead to a tunable optical delay scanning at 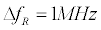, with a maximum delay equal to 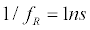(equivalent to a linear translation delay line with a 15-cm depth in free space) and a temporal resolution of 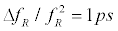. Such a combination of high scan rates and large scan depths makes ASOPS an ideal option for real-time, in situ interferometry, spectroscopy and imaging [3-8].

Figure 1: The basic operation principle of ASOPS: (a) Two pulse trains with slightly detuned repetition rates create a periodic scan of the relative pulse delay (time-domain Vernier effect). (b) In the frequency domain, two optical frequency combs with slightly different line spacings beat each other and generate a third frequency comb in the radio-frequency domain. Note that, in actual ASOPS systems, depending on the requirements of specific applications, the pulse repetition rates and/or the optical phases of the two lasers may have to be locked via active feedback control [7,18].

Optical sampling based on asynchronous pulsed lasers was first reported by Duguay and Hansen in 1968 [4]. The name of ASOPS was coined in later by [5]. While early work on ASOPS primarily focused on optical waveform characterization [6] and time-resolved spectroscopy [7, 8], recent years have seen a rapid expansion of the application scope of ASOPS. This is largely due to the advent of femtosecond optical frequency combs (OFC) [9]. An OFC is a femtosecond laser with highly stable repetition rate and optical phase. Because of this superb stability, the spectrum from an OFC consists of a grid of equidistant spectral lines, forming a so called “comb”. The spacing between adjacent spectral lines is equal to the pulse repetition rate. When the outputs of two identical OFC lasers with slightly detuned repetition rates are combined, the beating between the two sets of comb lines leads to a third comb, which is down-shifted to the radio-frequency (RF) range as illustrated in Figure 1b. This allows amplitude and phase information in the optical domain to be mapped into the RF domain, where precision measurements are much easier to make. As a result, “dual-comb” ASOPS is especially suitable for metrological applications.

One of the areas that have attracted a lot of interest in recent years is dual-comb ranging and lidar (laser radar) [10-14]. This is driven by the desire for the ability to track the positions of high-speed targets at distances with sub-wavelength accuracies, which requires a unique combination of rapid scans, long nonambiguity ranges (NAR) and fringe-resolving interferograms. The first report of dual-comb ranging was made by [10]. Their scheme used an ASOPS system with two phase-locked OFCs and combined both a time-of-flight measurement (for coarse scaling of distance) and an interferometric measurement (for highresolution length metrology). A 5-nm precision was achieved in 60 ms for an equivalent free-space target distance of 1.8 km, and the scheme is potentially capable of reaching a fractional ranging resolution on the order of 1×10⁻¹³ over 30 km. Scanning at about 5 kHz, their system also demonstrated the potential to track line-of-sight motions of a target as fast as 3.7 km/s. A later report from the same group simplified the scheme by using two free-running femtosecond lasers and achieved improvements in acquisition time and dead zones [11]. Similar experiments were also reported by Lee et al. with a 69-m target distance in open air [12]. More recently, type-II second harmonic generation has been used in conjunction with ASOPS to simplify absolute-distance calculation [13]. Meanwhile, dual-comb ASOPS has also served as the platform for many-wavelength interferometry in absolute distance measurement [14].

Another area where the dual-comb method has made a huge impact is spectroscopy. Because of the frequency “down-shift” mentioned earlier, spectral features in the optical domain can now be characterized in the RF domain with unprecedented accuracy, effectively merging spectroscopy with frequency metrology. The concept of dual-comb spectroscopy was first proposed by Weide and Keilmann in 1998 [15] (also independently by Schiller in 2002 [16]). Several groups subsequently reported experimental demonstrations of the scheme [17-24]. Notably, Coddington et al. demonstrated a multiheterodyne scheme capable of resolving each individual comb mode (100 MHz apart) with hertz-level accuracy [17, 18]. In recent years, dual-comb spectroscopy has merged with conventional spectroscopic techniques such as cavity-ring-down spectroscopy [19], coherent anti-Stokes Raman spectroscopy [20], and mid-infrared spectroscopy [21-23] to branch into broader areas and has entered the main-stream market as commercial products.

Despite its all-around superiority over conventional techniques, ASOPS nevertheless has some drawbacks. The requirement for two OFC lasers adds a major cost to the scheme. For applications relying on interference between the two frequency combs, a phase-lock system must be used to maintain the phase coherence between the lasers, which introduces additional complexity.

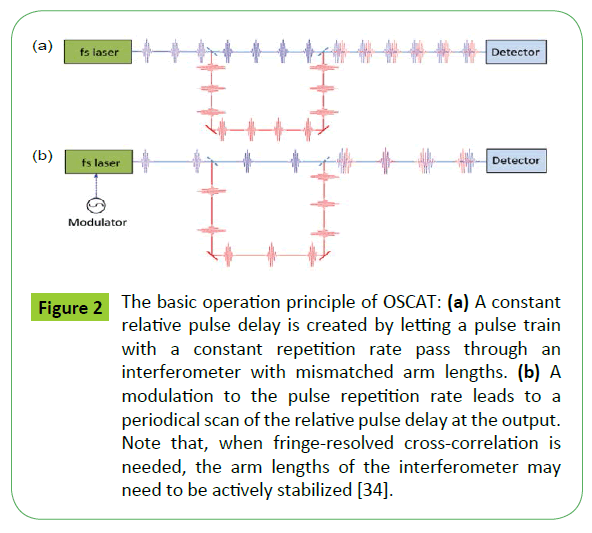
To address these problems, an alternative optical-sampling approach has recently been developed. It is called optical sampling by cavity tuning (OSCAT) [25-34]. The chief goal of OSCAT is to alleviate the need for two femtosecond lasers while retaining the ability to make deep and rapid scan of the relative pulse delay. This is accomplished by combining laser intra-cavity modulation with an arm-length mismatched interferometer [25, 30]. The intra-cavity modulation, typically a cavity-length modulation by means of a piezo-electric (PZT) actuator, tunes the pulse repetition rate. When such a pulse train travels through an interferometer with different arm lengths, as shown in (Figure 2), a time-varying relative pulse delay is created at the output end. The rate of this delay scan is equal to the intra-cavity modulation frequency and the scan depth Δl_d (i.e., the maximum relative pulse delay in terms of free-space length) can be approximately written as 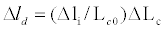, where 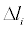is the mismatch of the interferometer arm lengths, 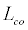is the nominal laser cavity length, and 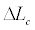is the cavity-length modulation depth [30]. With optical fiber interferometers, 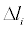can easily be at the kilometer scale or longer. 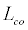, on the other hand, is typically 0.1–1 m so that the ratio 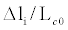is 103–104. This means that a 10-μm variation of the cavity length is able to produce a relative pulse delay as large as 10 cm! In essence, the OSCAT scheme creates a scale converter that “amplifies” a small displacement of the PZT to attain a large effective displacement in pulse relative positions. The implication of this scale conversion is profound because, although PZT actuators are still mechanical systems, the much-reduced depth requirement opens up possibilities for much higher tuning frequencies. For example, typical mirror-mounted PZT actuators have bandwidths in the order of 10 kHz and intra-cavity tuning as fast as 180 kHz has been experimentally demonstrated [35]. In addition, since the two pulse trains in OSCAT come from the same laser, they are coherent to each other so long as the arm-length mismatch of the interferometer does not exceed the coherence length of the laser (typically a few kilometers). These features make OSCAT a cost-effective alternative to ASOPS for a wide variety of applications.

Figure 2: The basic operation principle of OSCAT: (a) A constant relative pulse delay is created by letting a pulse train with a constant repetition rate pass through an interferometer with mismatched arm lengths. (b) A modulation to the pulse repetition rate leads to a periodical scan of the relative pulse delay at the output. Note that, when fringe-resolved cross-correlation is needed, the arm lengths of the interferometer may need to be actively stabilized [34].

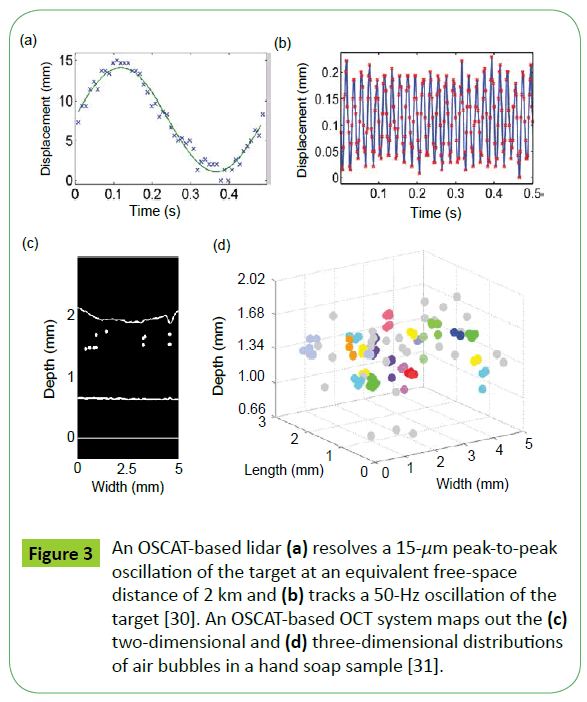
Early work on OSCAT focused on proof-of-principle demonstrations of the technique in pump-probe spectroscopy [26], terahertz spectrometry [27] and Fourier-transform spectrometry [28]. We reported the first application of OSCAT in ranging, using it as a lidar to track the dynamic motions of a target and to measure the absolute distance of the target [30]. Target vibrations as small as 15 μm peak-to-peak and as fast as 50 Hz were successfully tracked by the lidar from an equivalent free-space distance of 2 km Figures 3a and 3b. Later, same principle was used to gauge much shorter distances in a demonstration of OSCAT-based optical coherence tomography (OCT) and surface profilometry [31]. Figures 3c and 3d show the two-dimensional and three-dimensional OCT images of air bubbles scattered in a hand soap sample [32]. OSCAT has also been used to recover human voice signals by tracking surface vibrations [33]. More recently, high-resolution Fourier-transform spectroscopy has been demonstrated using an OSCAT system [34]. Spectral resolutions as high as 0.5 GHz are realized over an 8-THz bandwidth and a 0.02-fs temporal accuracy is achieved in interferograms sampling.

Figure 3: An OSCAT-based lidar (a) resolves a 15-μm peak-to-peak oscillation of the target at an equivalent free-space distance of 2 km and (b) tracks a 50-Hz oscillation of the target [30]. An OSCAT-based OCT system maps out the (c) two-dimensional and (d) three-dimensional distributions of air bubbles in a hand soap sample [31].

Compared to ASOPS, OSCAT is still in its early stage of development. Some key technical challenges are yet to be fully addressed. For example, to ensure stable pulsing under intra-cavity modulation, it is advantageous to use lasers with short cavities and high repetition rates. Thus, cavity-tunable GHz femtosecond lasers are desired. In some applications, slow drifts of laser cavities can cause unwanted additional modulations to the repetition rates and active control of cavity lengths may be necessary to remove such drifts. Nonetheless, these solutions appear to be readily available with the current technology.

In summary, optical sampling based on the time-domain Vernier effect has emerged as a powerful technique for metrological applications. Both ASOPS and OSCAT have demonstrated potentials to perform length metrology and frequency metrology. With proper transducers to convert other physical quantities to time and frequency, it is conceivable that these techniques may have even broader impacts on precision measurement.

Acknowledgement

This work was supported in part by the National Science Foundation under Grant ECCS-1254902, in part by the National Aeronautics and Space Administration through the Experimental Program to Stimulate Competitive Research under Grant NNX13AB09A, and in part by the Alabama Graduate Research Scholars Program.

References

1. Berrettini G, Bogoni A, Fresi F, Meloni G, Potì L (2010)Evolution of Optical Sampling. In:Costa N, Cartaxo A, eds. Advances in Lasers and Electro Optics. Croatia: INTECH 2010:289-314.
2. Hänsch TW (2006) Nobel Lecture: Passion for precision. Rev Modern Phys78:1297-309.
3. Kray S, Spöler F, Först M, Kurz H (2008) Dual femtosecond laser multiheterodyne optical coherence tomography.OptLett 33:2092-2094.
4. Duguay MA, Hansen W (1968) Optical Sampling of Subnanosecond Light Pulses Appl Phys Lett 13:178-180.
5. Elzinga P, Lytle FE,Jian Y, KingFB, LaurendeauNM (1987) Pump/Probe Spectroscopy by Asynchronous Optical Sampling. Applied Spectroscopy 41:2-4.
6. KanadaT,FranzenDL (1986) Optical waveform measurement by optical sampling with a mode-locked laser diode. OptLett 11:4-6.
7. JankeC, FörstM, NagelM, KurzH (2005) Asynchronous optical sampling for high-speed characterization of integrated resonant terahertz sensors. OptLett30:1405-1407.
8. BartelsA, CernaR, KistnerC, ThomaA, HudertF, et al. (2007) Ultrafast time-domain spectroscopy based on high-speed asynchronous optical sampling. Review of Scientific Instruments 78:1-8.
9. Ye J,Cundiff ST (2005) Femtosecond optical frequency comb: principle, operation and applications.
10. CoddingtonI, SwannWC, NenadovicL, NewburyNR (2009) Rapid and precise absolute distance measurements at long range. Nature Photonics 3:351-356.
11. LiuT, NewburyNR, CoddingtonI (2011) Sub-micron absolute distance measurements in sub-millisecond times with dual free-running femtosecond Er fiber-lasers. Opt Express 19:1-9.
12. LeeJ, HanS, LeeK, BaeE, Kim S, et al. (2013) Absolute distance measurement by dual-comb interferometry with adjustable synthetic wavelength. Measurement Science and Technology 24: 1-8.
13. ZhangH, WeiH, Wu X, Yang H, Li Y (2014)Absolute distance measurement by dual-comb nonlinear asynchronous optical sampling. Opt Express 22:6597-6604.
14. van den Berg SA, Persijn ST, Kok GJP, Zeitouny MG, Bhattacharya N (2012) Many-Wavelength Interferometry with Thousands of Lasers for Absolute Distance Measurement. Phys Rev Lett 108:1-5.
15. van der Weide DW, Keilmann F (1998) inventors;Max-Planck-GesellschaftzurForderung der Wissenschaften, assignee. Coherent periodically pulsed radiation spectrometer. United States patent.
16. Schiller S (2002) Spectrometry with frequency combs. OptLett27: 766-768.
17. Coddington I, Swann WC, Newbury NR (2008) Coherent Multiheterodyne Spectroscopy Using Stabilized Optical Frequency Combs. Phys Rev Lett 100:1-4.
18. Coddington I, Swann WC, Newbury NR (2010)Coherent dual-comb spectroscopy at high signal-to-noise ratio.Phys Rev A82:1-13.
19. Bernhardt B, Ozawa A, Jacquet P, Jacquey M, Kobayashi Y, et al. (2010) Cavity-enhanced dual-comb spectroscopy. Nature Photonics 4:55–57.
20. Ideguchi T, Holzner S, Bernhardt B, Guelachvili G, Picqué N, et al. (2013)Coherent Raman spectro-imaging with laser frequency combs. Nature 502:355-358.
21. Keilmann F,Gohle C, Holzwarth R (2004) Time-domain mid-infrared frequency-comb spectrometer. OptLett 29:1542-1544.
22. Schliesser A, Brehm M, Keilmann F, van der Weide DW (2005) Frequency-comb infrared spectrometer for rapid, remote chemical sensing. Opt Express 13:9029-9038.
23. Bernhardt B, Sorokin E, Jacquet P, Thon R, Becker T, et al. (2010)Mid-infrared dual-comb spectroscopy with 2.4 µm Cr2+:ZnSe femtosecond lasers. Appl Phys 100:3-8.
24. Zhu F, Mohamed T, Strohaber J, Kolomenskii AA, Udem T, et al. (2013)Real-time dual frequency comb spectroscopy in the near infrared. Appl Phys Lett 102:1-4.
25. Hochrein T, Wilk R, Mei M, Holzwarth R, Krumbholz N, et al. (2010) Optical sampling by laser cavity tuning.Opt Express 18: 1613-1617.
26. Wilk R, Hochrein T, Koch M, Mei M, Holzwarth R (2011) OSCAT: Novel technique for time-resolved experiments without moveable optical delay lines.J Infrared Milli Terahz Waves 32:596–602.
27. Wilk R, Hochrein T, Koch M, Mei M, Holzwarth R (2011) Terahertz spectrometer operation by laser repetition frequency tuning.J Opt Soc Am B  28:592-595.
28. Romann A, Mohr C, Ruehl A, Hartl I, Fermann ME (2011) Mode-Locked Yb-Fiber Laser for Rapid Dual Pulse Scanning Applications.in Advances in Optical Materials, OSA Technical Digest (CD) (Optical Society of America, 2011), paper JWA2.
29. Potvin S, Boudreau S, Deschênes JD, Genest J (2013)Fully referenced single-comb interferometry using optical sampling by laser-cavity tuning.Appl Opt 52:248-255.
30. Yang L, Nie J, Duan L (2013) Dynamic optical sampling by cavity tuning and its application in lidar.Opt Express 21:3850-3860.
31. Yang L, Duan L (2015) Depth-Resolved Imaging Based on Optical Sampling by Cavity Tuning. IEEE PhotonTechnolLett27: 1761-1764.
32. YangL, Duan L (2015) Optical coherence tomography and profilometry based on optical sampling by cavity tuning, in Frontiers in Optics 2015, OSA Technical Digest (online) (Optical Society of America, 2015), paper FW4E.4.
33. Boudreau S, Genest J (2014) Range-resolved vibrometry using a frequency comb in the OSCAT configuration.Opt Express 22:8101-8113.
34. Lee K, Lee J, Jang Y, Han S, Jang H, et al. (2015) Fourier-transform spectroscopy using an Er-doped fiber femtosecond laser by sweeping the pulse repetition rate. Scientific Reports 5:15726.
35. Briles TC, Yost DC, Cingöz A, Ye J, Schibli TR (2010) Simple piezoelectric-actuated mirror with 180 kHz servo bandwidth.Opt Express 18: 9739-9746.