Metrological modeling of colorimetric measurements results of in hardware and software environments
Yauheniya Saukova
DOI10.21767/2472-1948.100006
Belorussian National Technical University, Minsk, Belarus
- Corresponding Author:
- Yauheniya Saukova
The Department “Standardization, Metrology and Information Systems”
the Instrumentation Engineering, Belorussian National Technical University
Minsk, Belarus
Tel: +375 29 6839006
E-mail: evgeniya-savkova@yandex.ru
Received date: February 10, 2016; Accepted date: February 29, 2016; Published date: March 07, 2016
Citation: Saukova Y. Metrological Modeling of Colorimetric Measurements Results in Hardware and Software Environments. J Sci Ind Metrol. 2016, 1:6. doi: 10.4172/2472-1948.100006
Abstract
The main development stages of the Colorimetry are described. The basic concepts and trends of modern colorimetry are defined. The definition of the term "High Resolution Colorimetry" as a new advance direction, based on the usage of rendering information systems and technologies of digital images processing is derived. Developed models of measurements results by the author are presented. They are the “base”, “fractal”, “information” and “complex” measurements results models which are got in hardware and software environments. The results of these investigations can be used in a control of the self-luminous and non self-luminous objects at all stages of their life cycle.
Background:
These researches are carried out within the scientific projects of the State Program "Electronics and Photonics", "Photonics 2015" and continue in 2016-2018 by the Program "Photonics and Opto - and Microelectronics". The author is one of the leaders of these projects. The main goal of the research is to develop metrological support of Colorimetry in software and hardware environments. The main hypothesis of research is “a digital images are information models of objects and sources of quantitative data about their properties”. However, it is necessary to take into account the loss of data in information systems. The author offers to use the model approach for estimation of measurement uncertainty using information entropy.
Methods and findings:
In the working process on the project both theoretical and experimental research methods based on scientific research laboratory of Opto-electronic instrumentation (Belarusian national technical University) and other leading lighting laboratories of Belarusian State Institute of Metrology, National Academy of Sciences of Belarus, etc. are used. The results of investigations suggest that the High Resolution Colorimetry can be applied to extended objects. Implemented the accuracy of photometric and colorimetric results measurements is ± 10 %. The developed methods are the basis for a methodology for measuring, registration and visual objects control using digital images. This methodology may be applicable to validation and verification of registration, display devices and test methods in accredited laboratories.
Keywords
Metrology; Measurements; Electronics and photonics
Introduction
The science and technique areas require the determination of the photometric and colorimetric objects parametersare developed at present. The control methods of color and brightness characteristics are used in medicine, machine and instrument engineering, chemical, food industry and others. New sources of radiation, materials and devices with the differentiated optical properties are developed. In construction new types of the coverings and textures influencing safety and esthetics of perception are created. Since the impact of lighting on neurobehavioral and visual functions of the human body is proven the real direction for specialists (such as lighting designers) is to do health and most comfortable light environment for work and rest due to optimization its photometric and colours parameters in real-time [1]. According to recommendations ISO/TK 452 it is necessary to control parameters of lighting devices and their near and far environment [2] taking into account aspects of safety and energy-saving.
Considering distribution of displays for personal and collective usage (from non self luminous reflecting screens to the self luminous extended objects - plasma (gas-discharge), video terminals and board with cluster LED structures) working in difficult weather conditions omit of monitoring of their ergonomic parameters – the brightness and color characteristics at all stages of life cycle. The complexity of the research objects, increasing their potential risk must monitoring of their performance at all stages of the life cycle. At same time create information technologies and digital devices promotes the development of promising methods of measuring control based on digital registration of objects and the processing of digital images, increasing the efficiency and informativenes of measurement and control operations. In this regard the High Resolution Colorimetry is a very important direction. Obviously such methods require the development and application of correct metrological support in terms of uncertainty estimation. This paper presents a brief analysis of the regulatory framework and the systematized main approaches to uncertainty estimation, proposes comprehensive models of the measurements results in information systems.
Basic Concepts of Colorimetry
In accordance with [3] the colorimetry is a measurement of a color, which is carried out according to the accepted system of conventions (the international agreements). As a color is defined as feeling and the measured size, it can qualitatively be evaluated (subjective methods) and measured quantitatively (objective methods) [4] (Figure 1). Subjective methods are based on equalizing of colors before disappearance of their visual distinction by means of visual additive and subtractive colorimeters, color scales and atlases. Objective methods use the measuring instruments allowing to receive spectral functions of distributions of primary and secondary radiators and on their basis to determine coordinates of color and chromaticity [5].
The major role in development of colorimetry belongs to G. Grassmann developing the laws of colors addition [6]. Nueberg suggested dividing a process of researches and interpretation of color impacts on organs of vision into three levels [7]:
• physical (the optical phenomena arising at interaction of light radiation with objects in various environments and conditions of observation);
• physiological (impacts of optical radiation on the visual analyzer including light and color feelings);
• Psychological (the psychological feelings caused by influence of radiations with certain physical characteristics including environment).
The developments of these directions are continued. The normative documents confirm this fact. Subjective methods are used in the microbiological analysis, design, the chemical, textile industry, ecology. For example, according to [8] the natural color of water can be determined by visual equalizing with the standardized basic samples. Also Sorokin offered the method of definition of a whiteness of porcelain based on expert evaluation [9], etc.
Vyszecky in [10] divided the objective colorimetry characterizing as follows: “It is the instrument of forecasting, whether there will correspond each other on the color of two light streams (visual stimulus) with different spectral distributions of energy under the set conditions of observations; the forecast of definition by triple stimulus values of two visual stimulus and if triple stimulus values at one stimulus just the same, as well as at another, - color compliance is stated by the average observer with normal color sight". Thus, the basic colorimetry assumes the usage of standardized models of observation conditions and finds application in a control of production in medicine, chemical, paint varnish and polytrophic industry. Research methods of metals colorimetric properties are considered in Sokolov’s work when are described the colorimetric methods for research of river water influence oxidability and chromaticity [11]. Voronin developed the methods and means for expeditious identification of species of wood [12]. Colorimetric methods of space objects (galaxies and nebulas) researches allow to get information about distributions of energy in their range, absolute value and temporary characteristics of variability are described in Parmasyan's and Shapovalova's works [13].
According to Vyshetski the highest colorimetry “includes methods are based on assess the color stimulus perception vision to the observer in a difficult environment which we see in every life”, that’s why it is an actual practice observation. The problem of color reproduction correction and perception becomes complicated as information volume increases at reproduction of the color image (a reproduction, the color photo, the image on the screen of TV-set or computer). Reliability of a color rendition of people can judge, generally relying on the memory (if at this moment it doesn't see the original). Therefore in this case it is necessary to offer a process of independent color reproduction hardware [14]. Methods of color information transfer by images in telecommunication systems are based on application of the highestcolorimetry. The important tendency of these systems improvement is the recognition of characteristics of the visual perception and conditions, including colorimetric parameters of an environment [15].
Faircheld in [16] entered concepts of "absolute" and "relative" colorimetry couples capabilities of color reproduction of technical means. If the output device has wider range, than an first profile, that is all colors are presented on the entrance can be displayed at the exit, visualization by means of absolute colorimetry (the colors which are behind limits of the reproduced color will be transferred to edge of a color range of the output device) with preservation "points white" is used. Relative colorimetry takes place at color transformations made by the color rendering systems, allowing displacing color in view of movement of "point of white" into new place due to limitations of color cover ages of technical devices.
According to the existing normative documents [17,18] modern methods of photometric and colorimetric measurements are based on determination of values of the measured values (brightness, luminous intensity, chromaticity coordinates) in the control points (sites) of objects. Shortcomings of these methods are the much duration caused by the consecutive mode of performance of measurements, impossibility to register the light distributions changing in time. In addition, the labor input connected with need of positioning of a measuring instrument for space before an extended surface of object, and need to switch ranges of measurements depending on values of the measured brightness.
At present the perspective control methods of objects are based on application of digital record keeping technologies with high three-dimensional resolution and images processing [19]. These methods assume making decisions on compliance / discrepancy of object to the established requirements for controlled parameter based on the graphic data that are read out from the display unit at measuring, visual and registration control. The first important problem is an ensuring metrological traceability in measuring control that assumes links to basic samples (standards, reference samples) by hierarchy of calibrations.
Considering the high cost and potential danger of research objects variety of means of the hardware and software includes into measuring system. There is an experience of determination of coordinates of chromaticity of production – non self- luminous objects, with use of systems of technical sight such as the medicine or polygraphy. The main stages of colorimetric development are shown in Figure 2.
However in this case the differential method of measurements based on determination of small color distinctions for narrow measuring tasks is the basis method. For the extended self luminous and non self-luminous objects with a range of brightness questions of metrological traceability are not solved because these methods are based on scales of order. Such scales do not allow getting reliable results because they have not a "fixed unit” and the condition of ensuring unity of measurements respectively isn't satisfied.
The second problem in Colorimetry is the question of characteristics rationing of light sources for their control. In relation to "white" light-emitting diodes for their sorting the IEC/PAS 62707-1 [20] and ANSI_ANSLG C78.377 [21] standards provided technologies of a binning of the plane of a color locus – allocation the of the tolerance areas (bins and opt bins) defining eight nominal rates of color temperature of absolutely black body. Binning of "color" light-emitting diodes is not realized yet. There are many of international organizations: the International Organization of Standardization (ISO), the International Union of Telecommunication (ITU), the International Electro technical Commission (IEC), the Commission International de l'Eclairage (CIE), the International Consortium of Color (ICC); and regional organizations: the European Broadcasting Union (EBU), the European Committee on Standardization (CEN), the European Committee on Standardization in Electrical Equipment (CENELEC), develop normative documents establishing requirements to photometric and to colors of the self- luminous and not selfluminous objects, methods of their reproduction and control and the recommendation about processing and interpretation of results of measurements.
At the State level scientific research is also conducted that find reflection in standards that show technical requirements and ways of photometric and colorimetric measurements. The harmonization processes of normative documents are observed in different countries on this subject. However the analysis of legislative base and results of scientific researchers is showed that they concern development of technical devices, technologies, hardware and the software for the solution of a certain narrow circle of measuring tasks in concrete areas.
Zuikov and Savkova [19] mean the new direction by colorimetry of high-resolution - the methodology of multiple parameter measurements and interdisciplinary area of researches. It is covering methods and measuring instruments, control and tests of the self-luminous and not self- luminous objects at all stages of their life cycle based on application of technologies of digital recordkeeping of objects with high three-dimensional resolution and processing of their digital images, allowing with the set level of reliability to give reliable results of measurements, control and tests. Prerequisites of development of colorimetry of highresolution - color television and the digital photo, complex control of the light environment, the information and advertising industry, development and reduction in cost of digital equipment that causes possibility of development of effective express control methods of photometric and colorimetric of objects. The one of main metrological tasks of high-resolution colorimetry is to design conditional scales in color spaces to measure color features of objects providing metrological traceability to reference standards or reference materials. This problem can be solved by using reference nonpoint sources as reference points of the scales.
Input Quantities and Theirs Description
For several decennary the concept of uncertainty has undergone significant changes. The regulatory framework at the international, regional and national levels was carried out simultaneously by different organizations. Recommendations INC-1 (1980) “Expression of experimental uncertainties" laid the basic principles of the model approach was the first document issued by the Working Group No. 1 on the basis of the Committee JCGM. Then after Revisions GUM (1992, 1995 and 2008) has developed seven additional documents [22] (VIM 3). There are over 102 normative documents at present. The analysis of these documents showed the total recommendations tailored to analytical measurements - Guides EURACHEM/CITAC; to calibrations and tests - EA-4/02, ILAC-P 10, ISO/TR 22971; Guides EURACHEM/EUROLAB/CITAC/NORDTEST, CEN/TS 15675 and other. Also, there is a transition from scalar to vector quantities and multiparameter measurements - ISO 17450-2. More attention is paid to modeling, microbiological counting - ISO 29201 and ambiguities – ISO 17450-2. In this regard, of particular relevance collation and aggregation of quantities, description of models with an unlimited number of input and output variables - JCGM 102 which is characteristic of information systems.
According to VIM 3 the quantity is the property of a phenomena, body or substance, which may be expressed quantitatively in the form of a number indicating the distinguishing symptom of as basis for comparison. Correct integration of the input quantities in the measurement process requires their classification state as true of the diversity and variety of nature. The concept of value in different areas of scientific knowledge has its specificity, determined by the subject research. The authors divided the values into three classes with respect to the measurements (Figure 3). Many of "Non-Archimedes" quantities are characterized by the fact that it is impossible them to apply the axiom of Archimedes-Eudoxus for them. Transformation "Non- Archimedes” values in other species are impossible to [23]. Scalars are the main variables for the quantitative description of models the objects’ properties in the measurement equation. Scalars can be divided into countable, proportional, additive, interval, and ratio quantitaties. Multidimensional values can be two-dimensional, three-dimensional and various other dimensions. In the general case, the logical value "more – less" hasn’t sense for multidimensional variables. The operations of addition and multiplication are specific to these quantities.
Thus, the sum of several non-zero vectors can be equal to zero and the product of vectors is a scalar and a vector [23]. The tensor is defined as a geometric object that describes a multidimensional array, i.e., a set of numbers, multiple indexes are numbered (n-dimensional table, where n is the valence of the tensor). So, the vector (tensor of rank) is a one-dimensional array (row or column), and objects such as linear operator and quadratic form or two-dimensional matrix. A scalar (a tensor of zero rank) is specified by a single number (which can be seen as a zerodimensional array with a single element). Scalars and vectors can be considered as special cases of tensors [24]. Each type of them is characterized by certain values scales. Multidimensional scales can be produced by combination of different types of scales. In the case of complex properties of the multidimensional scale combine of different information characteristics (size, function, functional, operator, etc.) in proper functional spaces [25].
The Principle of Measurement Result Modeling
The measurement result is a set of indicators:
• point estimate of the measurement result (arithmetic mean - mathematical expectation, mode, median);
• combined or an expanded uncertainty;
• the probability of coverage.
According to [22] the multivariate random variable is an ordered collection (vector) of a fixed number N of one-dimensional random variables. The vector of mean values and covariance matrix are the main numerical characteristics of the multidimensional random variable. A model of mathematical expectations (the vector of mean values) as follows for an n-dimensional value X:
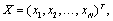 (1)
(1)
where 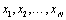 – input quantities.
– input quantities.
Covariance matrix (combined uncertainty) is described by the expression:
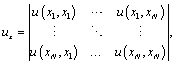 (2)
(2)
where 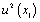 – the dispersion of an assessment x1;
– the dispersion of an assessment x1;
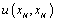 – the covariation.
– the covariation.
In mathematical and graphical interpretation the measurement result is transformed from the point with interval of the coverage to the point and the plane of reference for two-dimensional and three-dimensional quantities is an area coverage. The measurement result for complex models with an unlimited number of input and output quantities will be represented as a set of vector-columns and covariance matrices, which consist of covariance pairs increasing as the 2n number of input variables. The dimension of the covariance matrix increases with the number of input variables (the dimension of the vector) and therefore increases the number of covariance pairs. For example, for a one-dimensional size of the number of covariance is equal to unity for the two-dimensional to four, three-dimensional – nine, four, sixteen, etc. Thus the number of covariance increases with the square according to the expression n2, where n is a dimension when you increase the dimension of the vector. The determinant of the covariance matrix is the generalized variance of the random vector, which characterizes the measure of dispersion of a random n-dimensional vector. The description of models of the measurement result becomes more complicated when moving from simpler to more complex models from the point of view of the accuracy characteristics of measures of place and measures of dispersion. So for one-dimensional scalar quantities for direct measurements measure the place represents the sum of the mathematical expectation and the amendments resulting from different sources of origin. When indirect measurements which is the next step in the hierarchy, the mathematical expectation is determined from the functional dependence of the input and output variables. Multidimensional models of mathematical expectations including the results of indirect and direct measurements are described by a vector of mean values. As for scattering models, they likewise become more complex as the method of calculation, and by their geometric representation: from cut for scalar quantities to the geometric body in space (e.g., the ellipsoid for three-dimensional quantity).
The basic model
A graphical interpretation describing the multidimensional measurement result value is presented on Figure 4. As shown before the measurement result can be described by a mathematical model of expectations (to figure point estimates of the output value) and the scattering model (or total measurement uncertainty). As the basic model is offered to consider the mechanism of the formation interval of the coverage of the measured (output) scalar.
The "Fractal" model with an unlimited number of input and output quantities
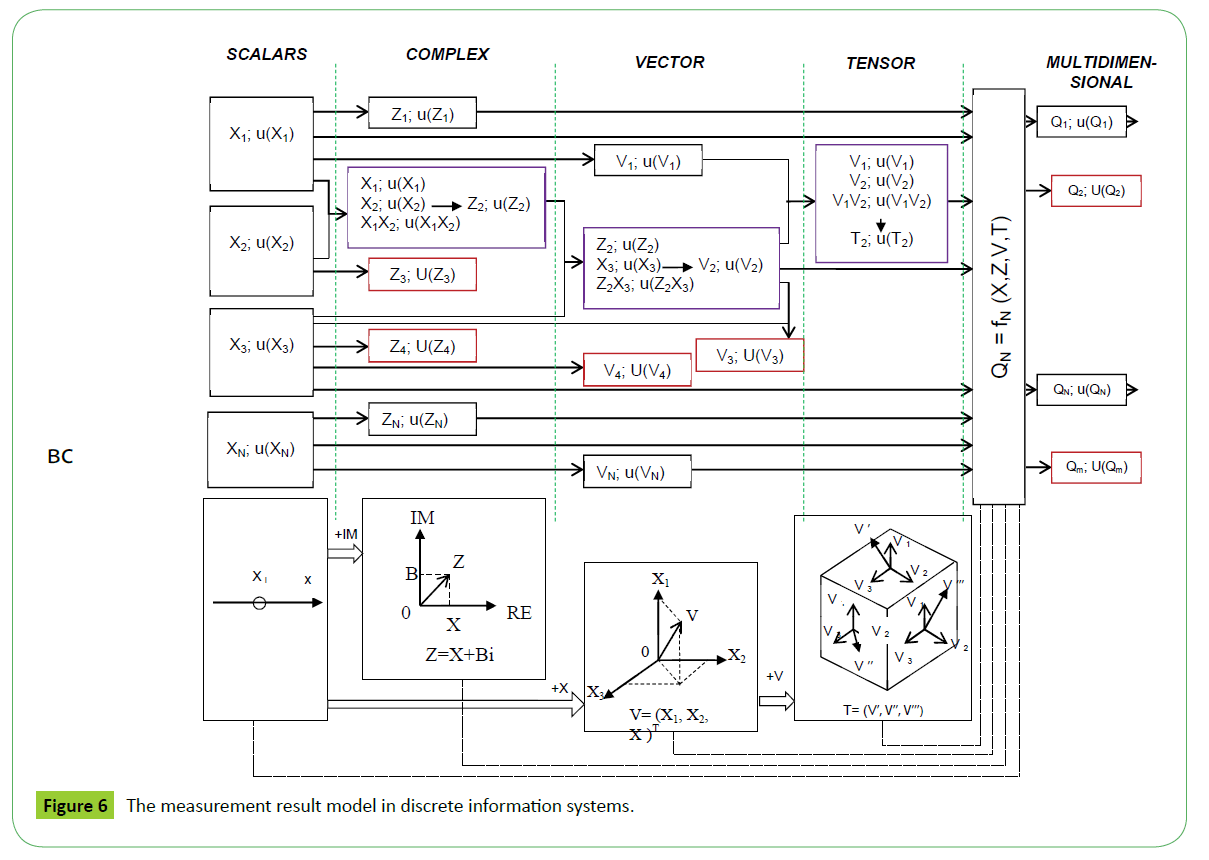
The model shown in Figure 4 is a special case and it can be considered as a submodel of the first, second and other levels describe measurements results in modern information systems. The author suggests using "fractal" model to describe the information-measuring systems with an unlimited number of inputs and output quantities. Graphical interpretation of "fractal" model is shown in Figure 5. This model is based on the idea of a fractal: the more "complex" sub-models are applied to more "simple" (top-down approach) as well as simpler models complexioned in models of higher levels (bottom-up approach) with almost no restrictions. Thus different input values can be fused during the measurement depending on measurement tasks. Each value can be measured (exits [ZN; U(ZN)]; [VN; U(VN)]; [TN; U(TN)]; [QN; U(QN)]) and can be fused with other variables acting together with their uncertainties in the inputs submodels of higher levels (entrances [ZN; u(ZN)]; [VN; u(VN)]; [TN; u(TN)]; [QN; u(QN)]). The modeling process of multidimensional measurement result values can be represented as a phase modelling results of different levels moving from direct and indirect measurements to multiparameter with unlimited number of input and output variables. The submodel of a certain level result can be decomposed into simpler sub-models of the lower levels and in turn is a subset of the models of a higher level.
Transformation of information using devices that are not measuring means (scanners, digital cameras, monitors, etc.) is a specificity of measurements in information systems. Therefore, it is necessary to consider the contributions of hardware and software at estimation uncertainty. It is obvious the dominant contribution of uncertainty is a methodical component. The author suggests using an information model based on entropy to describe the measurement results in information systems. According to [26], the entropy Н(р) of a discrete ensemble with a probability distribution p is a convex function of its argument p. In general the amount of information I obtained in the experiment, is defined as a measure of reduction of uncertainty, namely:
I = H - H0, (3)
where H – the entropy before the experiment;
H0 – the entropy after the experiment (residual).
Measurement of entropy (H=-p1log2p1- . . . - pnlog2(pn) applied to the information source can find the minimum bandwidth to reliably send information in the form of encoded binary digits. The measure of the Shannon entropy expresses the uncertainty of the random variable. Thus entropy is the difference between the information contained in the message, and that part of information which is known exactly in the message [27] (Figure 6).
As an example the vector quantity defined by using information systems that can result in a color. There are two approaches which identified to the definition of entropy images (RGB) in [28]:
• The image entropy is the sum of image channels entropic;
• The entropy of the image is determined depending on intensities of the colors (R, G, B).
In the first approach it is necessary to determine the entropy of each channel in the image to calculate the entropy of an entire image Н(Х). The vector С is the image channel X, С = {R, G, B}. Then the entropy of the image channel is determined by the Shannon formula:
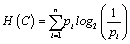 (4)
(4)
where C is the image channel;
pi– the probability is defined as the quotient from dividing the number of occurrences of the i-th byte (i = 0...255) in the image channel to the number of bytes of the channel C of the the image H.
Thus the evaluation of uncertainty is in obtaining quantitative information about the object based on digital images processing is a process of " black box unboxing " to identificate sources of data loss (and hence loss of precision) in the information channel. The relationship of information entropy and uncertainty was determined on the basis of application of mathematical apparatus of random number generators. It is established that entropic uncertainty interval covers only part of the distribution in which the majority of possible values of random error while some their share remains outside the boundaries of this interval.
Therefore the distribution can be specified as a value of confidence in which entropy and a confidence error values match [27]. This ratio is the formal definition of entropy of a random value:
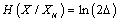 (5)
(5)
where H( X | XN) – a full residual entropy, bit;
X, XN – the current value of the measured value and the result;
Δ – the error, bit.
The entropy error range can be calculated as follows:
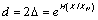 (6)
(6)
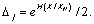
The correlation between error Δj and standard deviation σ of value for different laws of distribution can be described by the coefficient:
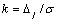 (7)
(7)
So for a rectangular distribution:
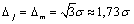 σ and therefore; k =1,73 .
σ and therefore; k =1,73 .
For a normal distribution:
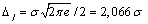 k = 2,066 .
k = 2,066 .
For atriangular distribution k =1,93 , for Laplace distribution k =1,93 , for axiological distribution k =1,11 , etc.
The entropy model
Presented equations have been expanded and adapted to the concept of "uncertainty". The expression that establishes the relationship between entropy and the uncertainty has the form:
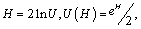 (8)
(8)
where U(H) – entropic uncertainty icoverage, bit.
On the base of data distributions the author built the dependencies capture the relationship between information entropy and uncertainty for different probability distributions (Figure 7).
It was found that the most “accurate” was a rectangular distribution:
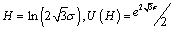 (9 )
(9 )
The probability distribution according to the Simpson law is described by the expression:q
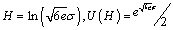 (10)
(10)
For normal law:
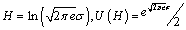 (11)
(11)
The application of information theory using entropy approach is a common way of describing and assessing the uncertainty of the measurement result is suitable for use in equal measure in both metric and non-metric scales. The proposed a graphical interpretation of entropy measurement result model in information systems is shown in Figure 8. In this case the external environment (for example lighting) on the original image and distorts it. In the future these distortions being a part of image information go through all stages of transformation (pre-filtering, sampling, quantization, encoding, etc.).
Also the internal environment (measuring information conversion) causes loss of accuracy of the measuring result.
Thus the measuring process of images color with the usage of the informative systems supposes additional parameters (the initial entropy of Н0, coloured coordinates of R0G0B0, the brightness of I0). An authentication and account of these parameters promote the exactness of measuring information.
The complex model
An author suggests entering a complex model uniting foregoing approaches and models for description of measuring result as it applies to the discrete informative transmitter systems. In this context equalization a measuring vagueness will be estimated by expression:
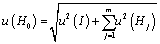 (12)
(12)
where u (I ) – the uncertainty of measuring information;
u(Hj) – the uncertainty of the j-th graphic data transformation in the discrete system.
An author suggests entering a complex model uniting foregoing approaches and models for description of measuring result as it applies to the discrete informative transmitter systems. In this context equalization a measuring vagueness will be estimated by expression. Taking into account different types of uncertainty evaluation (type A and type B), and also rectangular kind of distribution in the discrete systems, the model of dispersion for expression (10) will assume a view:
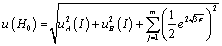 (13)
(13)
where σ – the standard deviation of the j-й input value is engaged in the process of transformation of information.
It is impossible to give graphic interpretations of results of the multiparametrical measurements in two- or three-dimensional presentation because they are difficult.
However we can see in literature two-dimensional analogues (models of Voronoy, Faircheld and other) for description of correlating sizes (Figure 9).
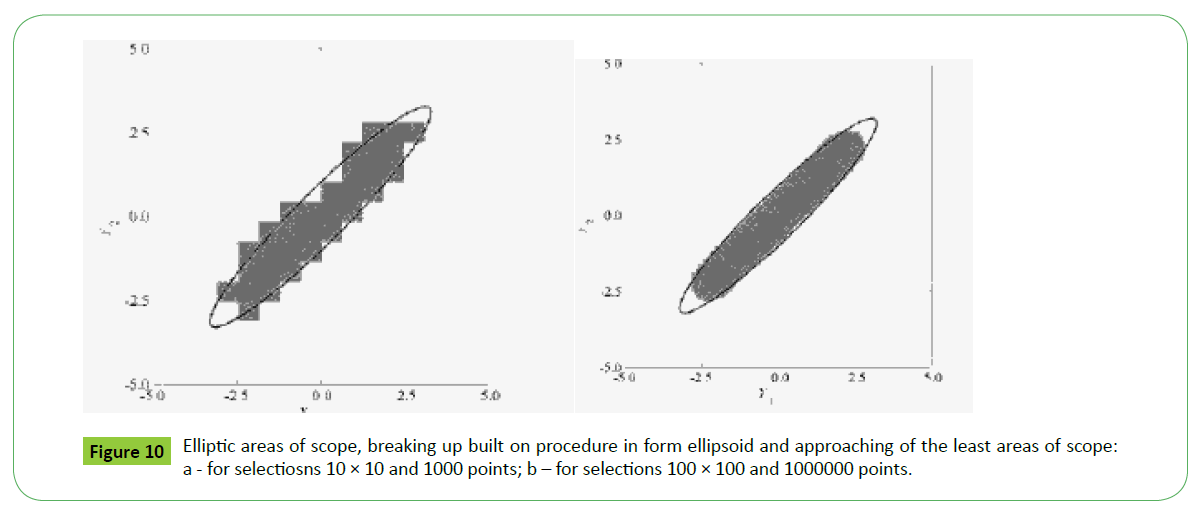
According to Figure 9 a measuring result is a plane of scope for the two-dimensional value (the model of Voronoy on Figure 9a and the triangulation model on Figure 9b) and an area of scope for the three-dimensional value (the GUM model on a Figure 9b and the Fershild’s model on a Figure 9d). The losses of information in the process of treatment result to reduction of amount of points and expansion of scope areas in the model of Voronoy. We can see the increasing of diameters described circumferences in a triangulation model. Failures of separate sectors are visible in the three-dimensional model of GUM. Areas of vagueness are laid on each other for the model Fershild’s model. Concordant [22] projection of areas of scope on a plane will be ellipses or parallelograms for the GUM model or more difficult figures in discrete systems as shown on a Figure 10.
Conclusion
In connection with application of the modern informative systems there are requirements in development of metrology vehicle for treatment and design of results of the multiparametrical measurements of multidimensional sizes. The results of these measurements are described of vector-matrixes (models of the expected values) and areas of scope of being a set variance-covariance matrices (models of dispersion).
The integrated approach to the measuring results modeling allows exposing the sources of changeability, on the basis of complication of input values as the submodels of different levels for the correct estimation of areas of scope.
It is offered to use the entropy model based on application of conditional scales of measurands providing metrology traceability for the evaluation of vagueness in the modern informative systems.
References
- General information (1965) Revisions; Corrigenda / Amendments.
- Design environment of buildings (2012)The internal environment of buildings. The design process for visual environment.
- International Lighting Vocabulary (2011).
- Shashlov A (2005) Lighting engineering Bases. M Science.
- Domasev MV, Gnatyuk SP (2009) Color, management of color, color calculations and measurements. St Petersburg 224.
- Gurevich M (1950) Color and his measurement. ML Publishing house of Academy of Sciences of the USSR268.
- Nyuberg ND (1947) Theoretical bases of a color reproduction. M The Soviet science 176.
- Scale of water colour. Technical conditions.
- International Lighting Vocabulary (2011).
- Vyshetski G (1973) Current developments in colorimetry. AIC Color 73: 21-51.
- Sokolov DI (2013) Influence of reservoirs on change of oxidability and chromaticity of river water (on the example of sources of water supply of Moscow). The abstract of the thesis on competition of an academic degree the edging ????? Sciences, Moscow, Lomonosov Moscow State University.
- Voronin AA (2011) Development and research of a spectral method and the equipment for expeditious identification of breeds of wood. Avtoreferet of the thesis St Petersburg, state university of informatics and technologies, mechanics and optics.
- Parmasyan ES, Shapovalova AI (1975)The abstract of the thesis on competition Detailed colorimetry of galaxies in the vicinity of NGC 1068 and irregular galaxies / Yerevan State University Yerevan.
- Lozhkin LD (2010) Differential colorimetry (Monograph). IUNL PGUTI 320.
- Kuznetsov YV (2005) Control systems of color: plan and opportunities. "Polygraphy" 4-5.
- Faircheld M (2013) Color appearance models, second Edition. Munsell Color Science Laboratory Rochester Institute of Technology, USA 3: 472.
- GOST R (2001) Means of display of information of individual use. Methods of measurements and assessment of ergonomic parameters and parameters of safety.
- GOST R (2001) Means of display of information of collective use. Requirements to visual display of information and ways of measurement.
- Zuikov I, Savkova E (2003) The colorimetry with a high dimensional resolution. Instruments and measurement methods. Scientific and technical journal Minsk Belarusian National Technical University1: 86-92.
- LED Binning General requirements and white grid (2011).
- American National Standard for Specifications for the Chromaticity of Solid State Lighting (SSL) Products (2011).
- International Vocabulary of Metrology: basic and general concepts and associated terms (2008).
- Evaluation of measurement data (2011) Supplement 2 to the “Guide to the expression of uncertainty in measurement” Extension to any number of output quantities 102.
- Uncertainty of measurement (2008) Part 3: Guide to the expression of uncertainty in measurement 98-103.
- Artemyev B, Vzorov V, Dmitriev A, Krasivskaya M, Yurin A (2014) About the scientific and technical concept of value. Main metrologist2.
- https://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BD%D0%B7%D0%BE%D1%80
- Sen N, Kotlyarov V, Grigoryev Y (2013) Application of estimations on the basis of entropy for comparison of cryptofirmness of cryptoalgorithms. Modern scientific technologies2.
- https://it.fitib.altstu.ru/neud/toiit/index.php?doc=teor&module=2
Open Access Journals
- Aquaculture & Veterinary Science
- Chemistry & Chemical Sciences
- Clinical Sciences
- Engineering
- General Science
- Genetics & Molecular Biology
- Health Care & Nursing
- Immunology & Microbiology
- Materials Science
- Mathematics & Physics
- Medical Sciences
- Neurology & Psychiatry
- Oncology & Cancer Science
- Pharmaceutical Sciences